Watching the 2018 Winter Olympics hosted in Pyeongchang inspired me to do a bit of analysis of curling. In this post we’ll examine the force balance of a moving stone as well as it’s trajectory without sweeping.

Without drag from the air and a level surface, I imagine a force acting on the stone with 2 components. The first is friction against the thrown direction of motion, the second is friction against rotation (curling).

The equation for the rotational frictional force acting on the stone becomes:

$$F_{f} = \mu mg (-\sin(\theta)\hat{i} + \cos(\theta)\hat{j})$$

and for the linear friction:

$$F_{l} = - \mu mg \hat{i}$$

where $\hat{i}$ represents the direction of the target area (positive east), and $\hat{j}$ represents the direction perpendicular to the target area (positive to the north).

The initial energy in the stone is a combination of linear and rotational kinetic values.

$$KE_{linear} = 1/2 m v^{2}$$ $$KE_{rotational} = 1/2 I \omega^{2}$$

Both of these quantities are reducing due to the frictional forces acting upon the rock.

Plotting the surface tractions related to these forces gives a sense of what is going on around the stone. Notice at the center of the South side has two opposing forces.

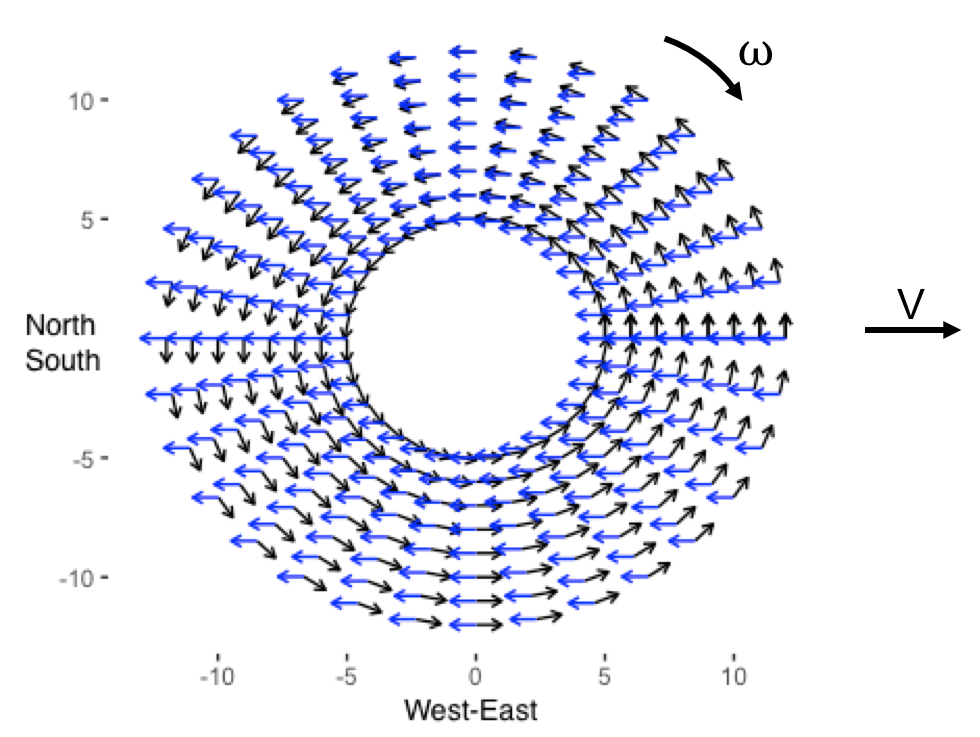
Computing the local combination of forces across the surface of the rock gives the following map:

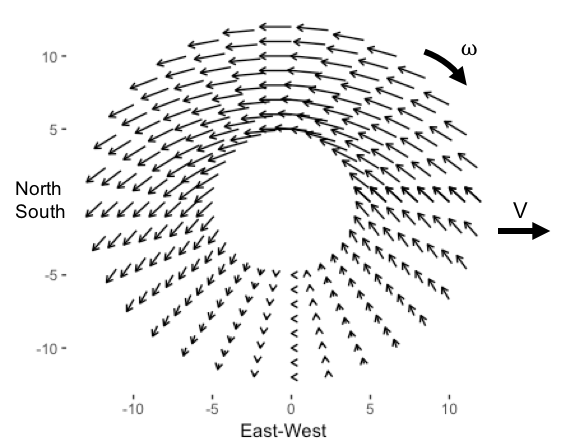
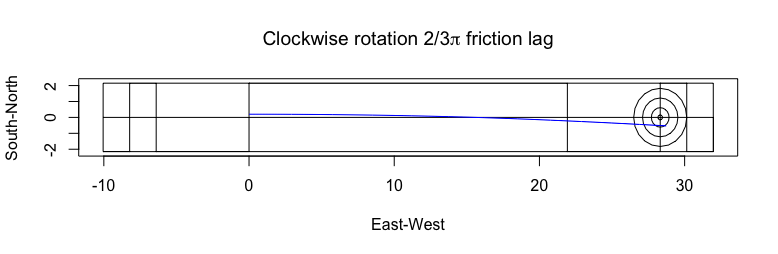
A force balance of these components would suggest the north side of the stone would slow down faster than the south side and cause the rock to curve opposite the rotation direction.

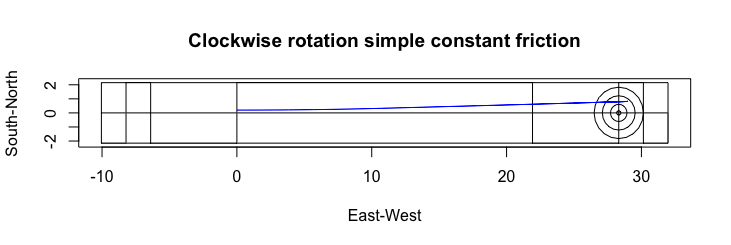
However, when you watch curling, the rocks curl in the same direction as the rotation. So, what is causing this trajectory?

To help solve this challenge, I’ll look at the interface of the ice and the rock.

The friction between the rock’s running band and the ice generates heat. This heat, along with the pressure of the rock melts the ice and alters the local coefficient of friction. I make a few simplifying assumptions about this mechanism and ignore local striations in the ice which could also contribute.

I define the coefficient of friction using polar coordinates and collapse the radial direction to a single distance. The local kinetic energy is assumed be the major factor generating heat and the reduction in friction coefficient is made proportional.

$$KE = KE_{linear} + KE_{rotational} \rightarrow \mu'(\theta,r')$$

Next, I rotate the coefficient of friction around the rock with a lagging angle relative to the local kinetic energy.

$$\mu(\theta,r) = \mu'(\theta-\phi,r)$$